Shop math: Practice makes perfect

Courtesy of All images: T. Lipton

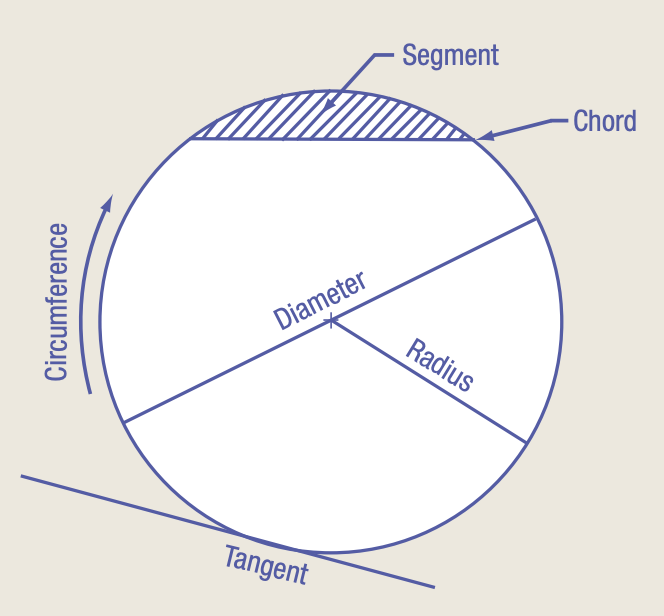
Terminology of a circle.

Shop math is an area where a little practice goes a long way. Over the years, I have found that many people became metalworkers because they hated math in school. This seems weird because of how much math the trade requires. If you want to get ahead and be one of the top dogs in a shop with your own bed and bowl, you will need some math in your toolkit.

I didn’t like math when I first started. My turnaround came when I found myself in a tight spot—I was tapped to teach basic shop math to a welding class. I tried to weasel out of the trap but there was no escape; everybody else had already out-weaseled me. The weekend before the class began, I hit the books hard to get a leg up on my students.

I discovered during that painful period that all I had to do was go slow and stay a little ahead of everybody else. I also learned two major lifetime nuggets teaching that class. First, as previously noted, a little practice is all it takes. A strong motivator, like having to chew your leg off to get out of a trap, also helps. The second nugget was the more you practice, the better you get. It sounds lame, but it’s true. Teaching that class several times firmly cemented the knowledge. It also gave me the confidence to go much further.

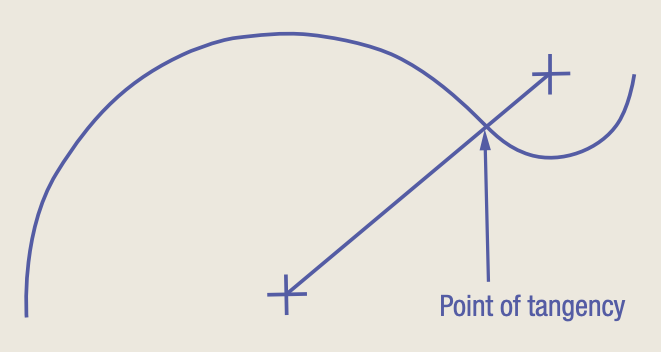
The line connecting the centers of the two arcs passes through the point of tangency.

Lacking this one skill has limited more tradesmen than I care to estimate. There is no reason for it other than lack of trying. In reality, there are a small number of concepts and formulas you actually need to memorize. The trick is to leverage what you have memorized to analyze other problems.

In addition to formulas, shapes are important to shop math, and the circle is one of the most important shapes encountered in the trades. It pays to know a few circle facts.

Every metalworker should know the terminology and properties of a circle. These come up so often during the course of everyday problem solving that metalworkers who don’t know them are handicapped.

A line tangent to any point touching a circle is perpendicular to the center of a circle at the point of tangency. This fact is useful when doing inspection and reverse engineering.

Knowing that two tangent arcs of different radii will have their centers along a common line passing through the point of tangency is also beneficial. Also, the length of any circular arc can be quickly calculated by multiplying the radius by the arc angle by 0.01745, or rα(0.01745) = arc length. You will see this number again, so it’s worth remembering.

Arc Length Calculator

Radius (r):
Angle (α) in Degrees:
Calculate Arc Length

Formula: Arc Length = r × α × 0.01745

Hopefully, everyone remembers that the circumference of a circle is the diameter multiplied by π, or C = d π.

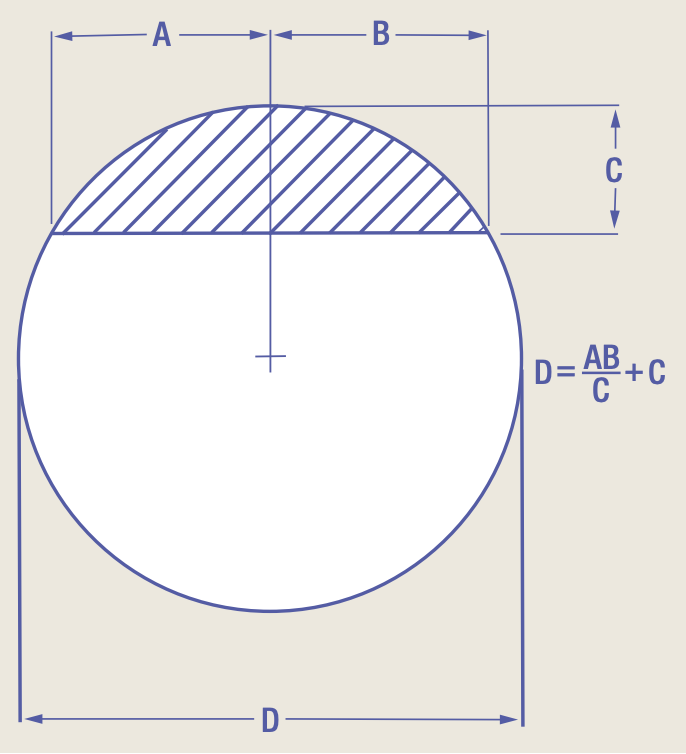
Measuring the chords of a circle. 

True roundness, or circularity, cannot be measured with a two-point measuring system. A common example is poor-quality, centerless ground shafts and pins. These will measure correctly with a two-point measuring tool like a micrometer, but when these pins or shafts are spun in a V-block and compared with an indicator, they show some roundness deviation as runout. The only true way to measure roundness is by rotation of an accurate spindle or center point.

The formulas for measuring chords are also extremely useful. I have used them often to find an unknown radius. Many times, things in the shop have a radius that is outside the range of standard radius gages.

Use a bar or pin of a known length to act as the chord for your measurement. Finding the radius can then be reduced to a simple calculation. The space between the pin and the radius to be measured can be determined with gage pins or by measuring the top of the pin with calipers. Be sure to measure in the center of the pin or bar to get the maximum measurement of the radius. A depth micrometer can also be used. The tip diameter of the depth micrometer will affect the depth measurement, but you can add a ball tip to the measuring tool to avoid that problem or to make some additional correction calculations for the tip diameter. CTE

Circle Chord Radius Calculator

Chord Length (c):
Height from Chord to Circle (h):
Calculate Radius

Formula: Radius = (c² / 8h) + (h / 2)

About the Author: Tom Lipton is a career metalworker who has worked at various job shops that produce parts for the consumer product development, laboratory equipment, medical services and custom machinery design industries. He has received six U.S. patents and lives in Alamo, Calif. Lipton’s column is adapted from information in his book “Metalworking Sink or Swim: Tips and Tricks for Machinists, Welders, and Fabricators,” published by Industrial Press Inc., New York. The publisher can be reached by calling (888) 528-7852 or visiting www.industrialpress.com. By indicating the code CTE-2010 when ordering, CTE readers will receive a 20 percent discount off the book’s list price of $44.95.