Balancing rotating elements in machines

The rotating elements in machine tools often generate unacceptable forces due to unbalance, and manufacturers usually take corrective action to reduce the forces. While it is unusual for end users to perform field balancing, manufacturers of machine tools, spindles, cutting tools, toolholders and other rotating equipment do it routinely. Balancing a thin, disc-like element such as a grinding wheel is often achieved through a procedure called “single-plane balancing.”

Unbalanced forces arise because the center of mass is not the same as the center of rotation. Figure 1 shows a thin disc (blue) mounted on a shaft (green) between two bearings (red). Because disc density is not perfectly uniform and the disc is not perfectly manufactured and perfectly mounted on the shaft, the center of mass is not the same as the center of rotation.

All images courtesy S. Smith

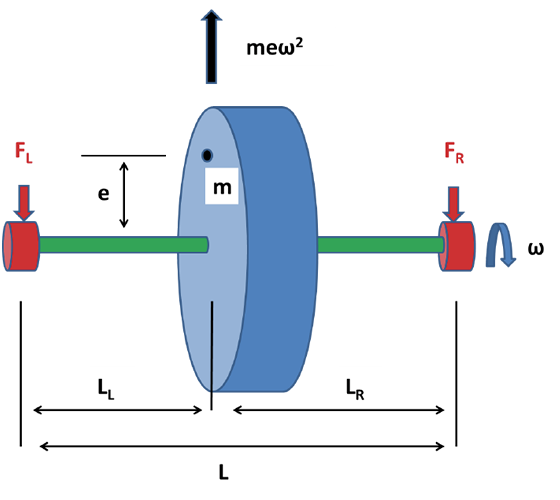
Figure 1. An unbalanced rotating element.

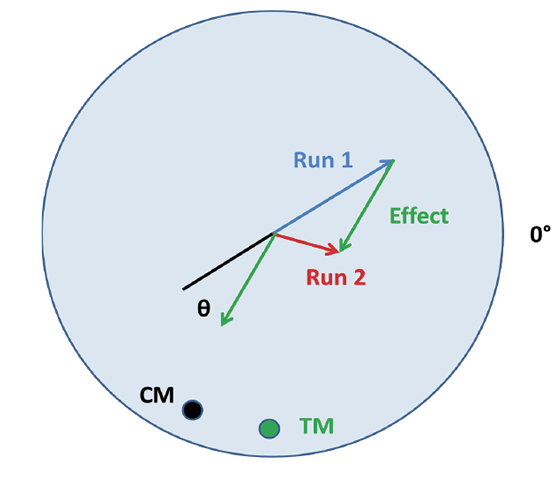
Figure 2. The balancing procedure using a trial mass.

It is convenient to think of the unbalance as a mass (m) off center by a distance (e) on an otherwise perfect wheel. As the shaft rotates at a speed (ω), the unbalanced mass generates a force equal to meω², and that force rotates with the disc. At the instant shown, the force pulls the wheel up. But after the shaft rotates 180°, the force pulls the wheel down. The resulting time-varying force causes the wheel to vibrate, and the goal of balancing is to eliminate or counteract the unbalance force. The force is proportional to the square of the rotational speed, so the importance of balancing increases dramatically as shaft speed increases.

Correcting the unbalance requires either adding an appropriate mass, such as a screw, to the light side or removing mass, such as by drilling a hole, from the heavy side. Many rotating elements have premanufactured threaded holes that accept balancing screws.